Demystifying Cycles in Graphs: A Union-Find Exploration

Our mission is to find out if a network of roads in a city forms a loop or not. In technical terms, we want to see if an undirected graph contains a cycle. If you process all the roads and don't find any loops, congratulations! You've found an acyclic graph.

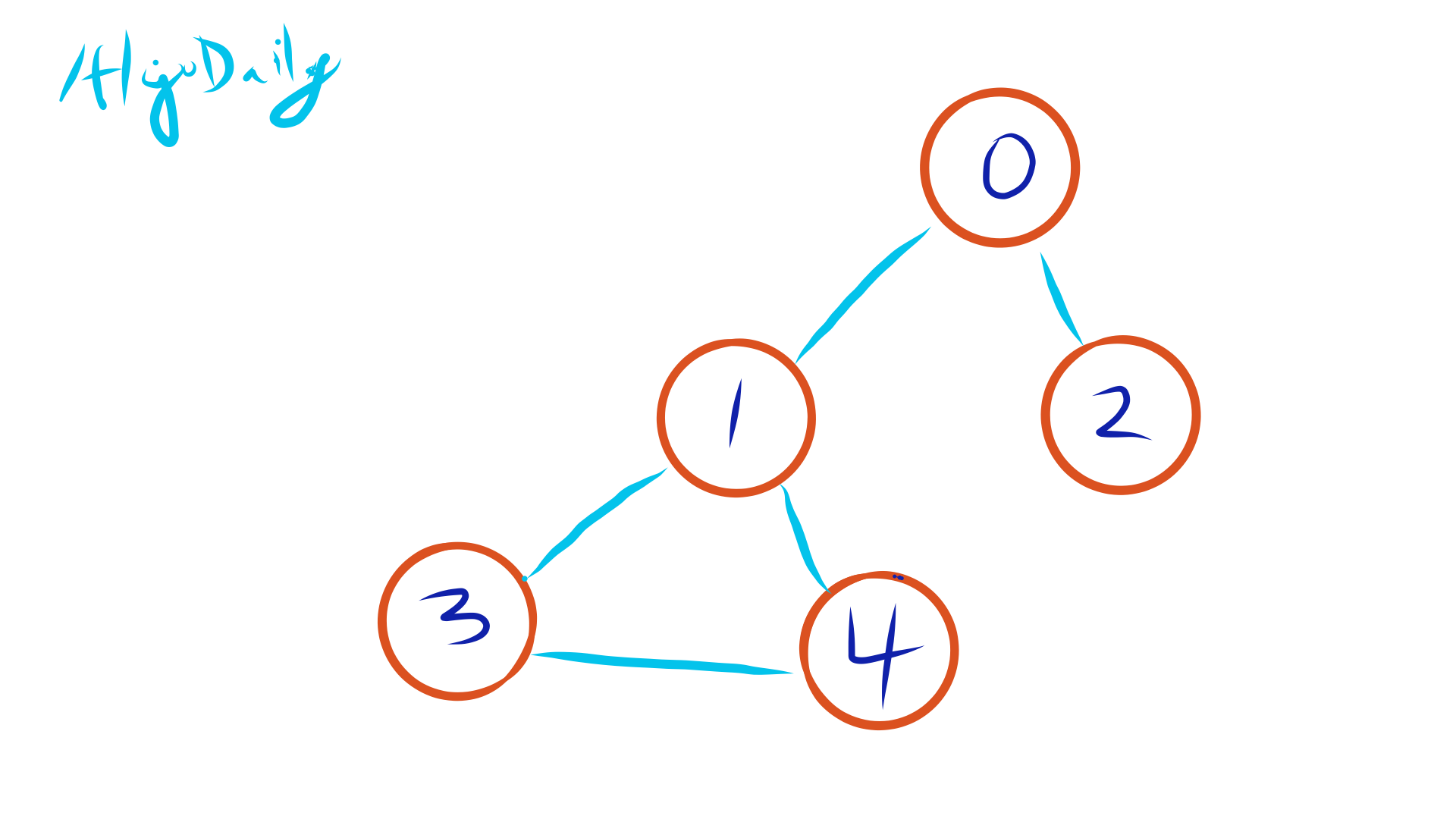
The Case at Hand: Does This Graph Have a Cycle?

Setting Up the Investigation Board: Initial Steps

First, let's consider each intersection (or vertex) as its own isolated neighborhood. To help us keep track of these neighborhoods, we'll use a 'parent array.'

Visual Snapshot of the Investigation Board

In this image, the number inside each circle represents a vertex, and the number below it signifies its 'parent.' Initially, each vertex is its own parent, representing isolated neighborhoods.

The Investigation Begins: Processing Edges

The First Clue: Edge (0,1)

Let's start with the road connecting intersections 0 and 1 and see if they're part of the same neighborhood.

What Did We Find?

1. Find(0) returns 0: Intersection 0 is its own neighborhood.
2. Find(1) returns 1: The same goes for intersection 1.

Since both intersections belong to different neighborhoods, there is no loop or cycle for this road.

We would continue this process for each road in our network. If we ever find a road where both intersections belong to the same neighborhood, that's our "Aha!" moment—a cycle is detected.

xxxxxxxxxx

// Initialize a parent array to represent isolated neighborhoods.

const parent = [0, 1, 2, 3, 4];

​

// Function to identify the 'root' or 'parent' of each neighborhood.

function find(vertex) {

    if (parent[vertex] === vertex) {

        return vertex;

    }

    return find(parent[vertex]);

}

​

// Let's check the neighborhoods of intersections 0 and 1.

const rootOfVertex0 = find(0);

const rootOfVertex1 = find(1);

​

console.log(`Find(0) = ${rootOfVertex0}`);  // Outputs: Find(0) = 0

console.log(`Find(1) = ${rootOfVertex1}`);  // Outputs: Find(1) = 1