Good evening! Here's our prompt for today.
Fizz Buzz is a classic interview question that apparently many experienced engineering candidates often can't solve! Let's cover it today.
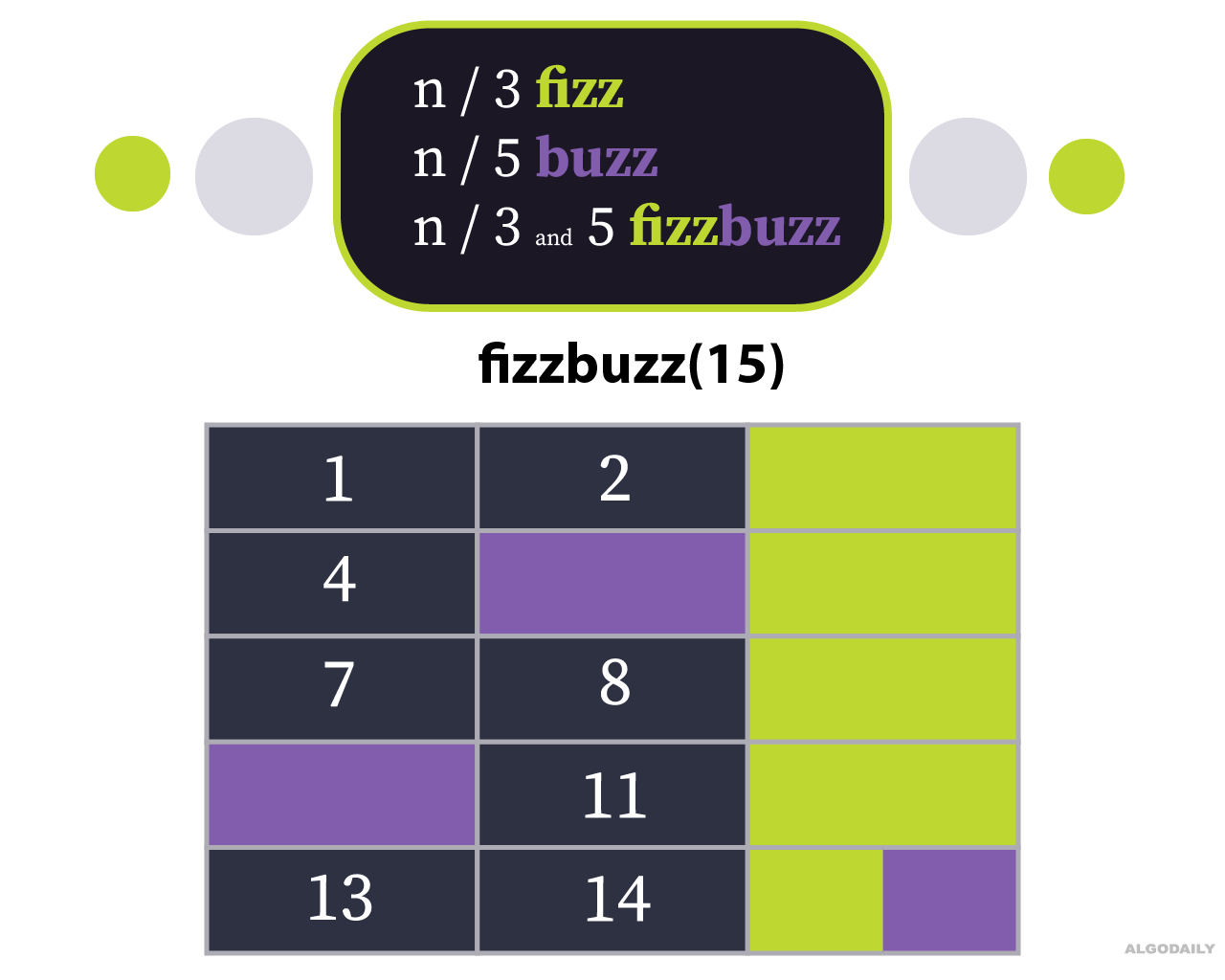
We're given a number in the form of an integer n.
Write a function that returns the string representation of all numbers from 1 to n based on the following rules:
If it's a multiple of 3, represent it as "fizz".
If it's a multiple of 5, represent it as "buzz".
If it's a multiple of both 3 and 5, represent it as "fizzbuzz".
If it's neither, just return the number itself.
As such, calling fizzBuzz(15) would result in '12fizz4buzzfizz78fizzbuzz11fizz1314fizzbuzz'.
The following image provides a visual of how we processed the input:
Constraints
- Maximum value of Integer
n<=1000 nwill always be a positive integer, but can be0- Expected time complexity :
O(n) - Expected space complexity :
O(1)
AlgoDaily partner CodeTips.co.uk has kindly provided a guide on solving Fizz Buzz in Go and Javascript. Check it out for even deeper coverage of this problem.
Try to solve this here or in Interactive Mode.
How do I practice this challenge?
xxxxxxxxxxstd::vector<std::string> fizz_buzz(int n) { // fill in return std::vector<std::string>();}TEST(test_1, fizz_buzz) { EXPECT_EQ(fizz_buzz(0), std::vector<std::string>());}TEST(test_2, fizz_buzz) { EXPECT_EQ(fizz_buzz(1), std::vector<std::string>({"1"}));}TEST(test_3, fizz_buzz) { EXPECT_EQ(fizz_buzz(15), std::vector<std::string>({ "1", "2", "fizz", "4", "buzz", "fizz", "7", "8", "fizz", "buzz",Here's a video of us explaining the solution.
To change the speed of the video or see it in full screen, click the icons to the right of the progress bar.
We'll now take you through what you need to know.
How do I use this guide?
Translating Decision Flows to Control Statements
Getting your dream software engineering job often involves cracking coding interviews, and the "FizzBuzz" problem is a classic example that tests your grasp of basic control flow. Let's delve into how to map the problem's requirements to technical implementations.
The Problem Statement Translated
The problem tasks you with making the following decisions based on the input number:
- Multiple of 3: Return "fizz"
- Multiple of 5: Return "buzz"
- Multiple of both 3 and 5: Return "fizzbuzz"
- None of the above: Return the number itself
Why Use Control Statements?
You might be wondering why control statements like if-else and switch are the way to go here. That's because these statements allow us to simulate decision-making in code, just as we do in everyday life. When your language doesn't include a switch statement, if-else ladders are the tool of choice.
The Art of Decision Making in Code
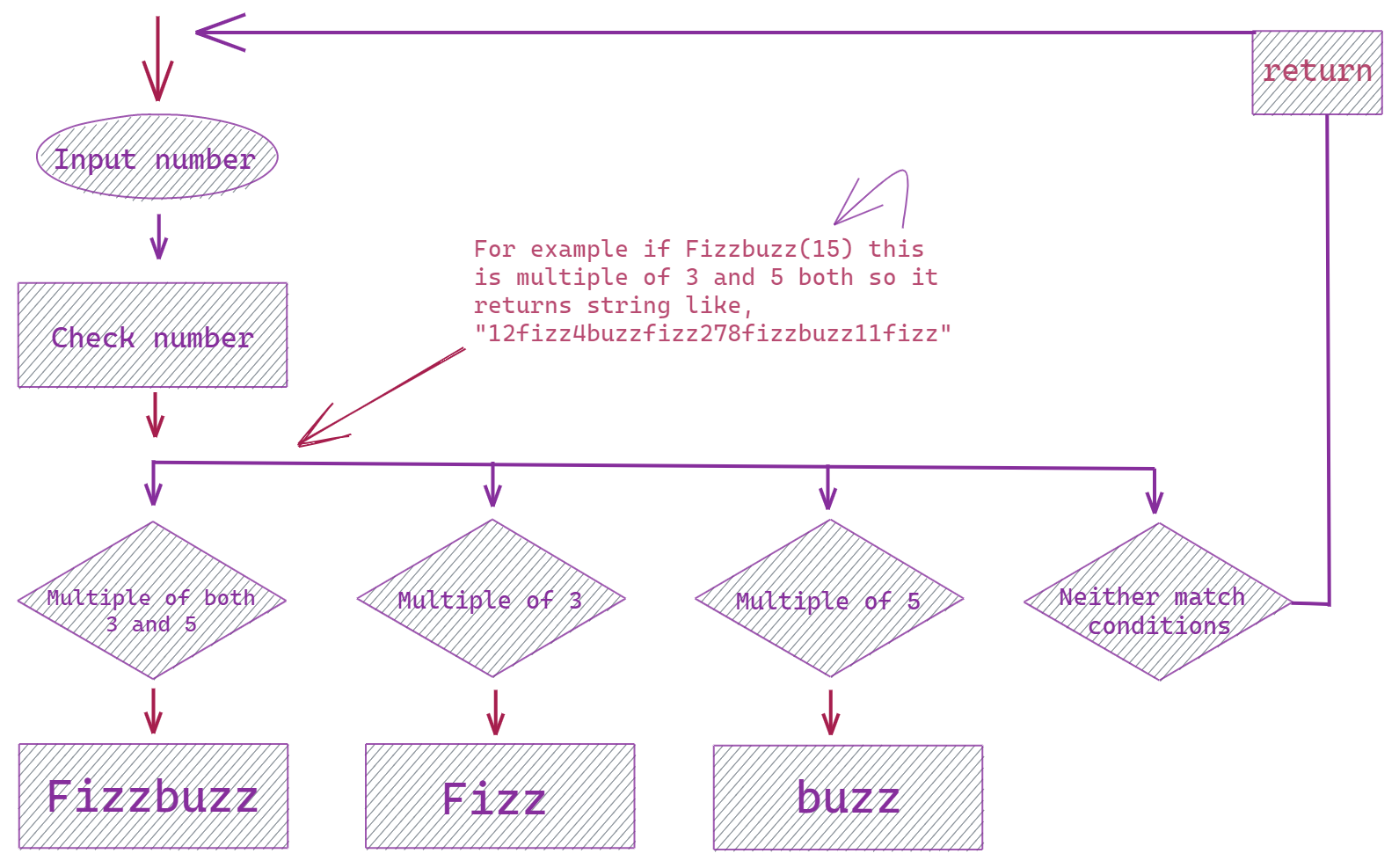
Step 1: Identify the Key Decisions
First, observe the series of decisions needed. Are they mutually exclusive? In our case, yes—each number can only map to one output. This screams "use an if-else ladder."
Step 2: Translate to if-else
Translate each decision point to an if-else statement.
- If a number is a multiple of both 3 and 5, the number is a multiple of 15 (
3 * 5). - To check if a number, say
n, is a multiple of another number, saym, we use the modulo operator%. Ifn % m == 0, thennis a multiple ofm.
1if (/* multiple of 3 */) {
2 // fizz
3} else if (/* multiple of 5 */) {
4 // buzz
5} else if (/* multiple of 3 and 5 */) {
6 // fizzbuzz
7} else {
8 // return number
9}Unveiling the Magic of the Modulo Operator
Just like you would use division in everyday math to find out if one number evenly fits into another, you can do the same in programming. However, there's a more elegant solution at hand: the modulo operator %.
A Visual Cue to Modulo Operation
Imagine the number 6 as a full container of water, and the number 3 as an empty cup. If you can pour the water into the empty cup such that the container becomes completely empty with no overflow or leftover, then it's safe to say 3 "neatly divides" into 6.
Why Division Falls Short
While division (/) can be used, it creates a mess. You'd need to deal with quotients and additional logic to make sense of any leftovers. This is like trying to use a measuring cylinder to manually calculate if the water can completely fill the empty cup, drop by drop.
Cumbersome, right?
The Power of Modulo (%)
Enter the modulo operator (%). This tool directly gives you any leftovers (the remainder) when you try to fit one number into another. If it gives you a zero, voila! The numbers fit perfectly.
Here's a quick example:
16 % 3
2// 0
3// 3 neatly divides into 6The Practicality of Modulo in the FizzBuzz Problem
For FizzBuzz, using % is an absolute win. Just check if the number, when divided by another (say 3 or 5), leaves a remainder of zero:
- If
n % 3 == 0, it's "fizz." - If
n % 5 == 0, it's "buzz." - If
n % 15 == 0, it's "fizzbuzz."
See? No mess, no fuss. Just a neat, simple solution for identifying multiples. And this, my friends, is why the modulo operator is your best companion for problems involving division and remainders.
Navigating the Maze of Conditionals: Order Matters!
Here's the classic pitfall.
The order of conditionals in FizzBuzz is an often overlooked detail that makes all the difference. Let's dive into understanding why the sequence is important, and then we can talk a bit about performance.
The Conditional Trap
Remember the earlier example where we used the following if-else ladder in various languages?
1if (num % 3 == 0) {
2 // fizz
3} else if (num % 5 == 0) {
4 // buzz
5} else if (num % 3 == 0 && num % 5 == 0) {
6 // fizzbuzz
7} else {
8 // return number
9}This isn't quite right!
Here's where many people also go wrong. Why? Because the order will short-circuit the fizzbuzz condition, which needs both 3 and 5 as divisors.
In our conditional, we'll want to address the fizzbuzz scenario first, since it needs to go before the fizz and buzz blocks. Because it is requires being divisible by both 3 and 5, it will get short circuited by either the 3 OR 5 cases first.
To restate, I mean that we need it to pass through the i % 3 == 0 && i % 5 == 0 condition before either of the individual % 3 or % 5 ones. Those cases are still true (and their logic will execute) even in cases where it's true for i % 3 && i % 5.
The time complexity is O(n) as it involves a single loop that iterates through each element once. When you're in a coding interview, pointing out the time complexity can score you extra points.
Some more helpful links:
One Pager Cheat Sheet
- We are given an integer
n, and asked to write a functionfizzBuzz()that returns the string representation of all numbers from1tonusing the rules "fizz", "buzz" and "fizzbuzz" for multiples of 3, 5 and both respectively, with a maximum value of1000,O(n)time complexity andO(1)space complexity. - The key to answering this technical interview question was to identify how to map a problem to its technical implementation, such as using
if-elseorswitchcontrol flows. - We can use the
modulo operator(%) to easily determine if one number is a multiple of another - the remainder returned will be0if it is. - We can use a conditional flow order of
fizzbuzz>fizz>buzz>return numberto check if a number is divisible by either3,5, both, or neither, with a time complexity ofO(n).
This is our final solution.
To visualize the solution and step through the below code, click Visualize the Solution on the right-side menu or the VISUALIZE button in Interactive Mode.
xxxxxxxxxx}std::vector<std::string> fizz_buzz(int n) { std::vector<std::string> ans; for (int i = 1; i <= n; ++i) { if (i % 3 == 0 && i % 5 == 0) { ans.push_back("fizzbuzz"); } else if (i % 3 == 0) { ans.push_back("fizz"); } else if (i % 5 == 0) { ans.push_back("buzz"); } else { ans.push_back(std::to_string(i)); } } return ans;}TEST(test_1, fizz_buzz) { EXPECT_EQ(fizz_buzz(0), std::vector<std::string>());}TEST(test_2, fizz_buzz) { EXPECT_EQ(fizz_buzz(1), std::vector<std::string>({"1"}));}TEST(test_3, fizz_buzz) { EXPECT_EQ(fizz_buzz(15), std::vector<std::string>({ "1", "2",You're doing a wonderful job. Keep going!
If you had any problems with this tutorial, check out the main forum thread here.


